Den zu diesem Journal gehörigen Podcast gibt es hier:
Bücher und BegriffeIch habe mir drei Bücher ausgesucht, mit denen ich die ersten Episoden bestreiten will. Danach können dann fortgeschritteneren Themen an die Reihe kommen. Dazu suche ich dann auch passendes Material heraus.
Als erstes möchte ich vergleichen, wie man so gemeinhin in die Materie einführt. Dazu beginne ich mit einem Buch, das wir im ersten Semester lesen sollten: Manfred Broys „Informatik 1 - Eine Einführung“.
Hier wird am Anfang den Begriff der „maschinellen Informationsverarbeitung“ definiert. Dieser gliedert sich bei Broy in die Darstellung und die Verarbeitung der Information. Bei der Darstellung handelt es sich um eine symbolische Repräsentation, die maschinell lesbar ist und die Verarbeitung erfolgt nach eindeutigen fixierten Regeln.
Donald E. Knuth (der Schöpfer des Schriftsatzsystems TeX) beginnt den ersten Band seines Buches „The Art of Computer Programming“ anders. Er konzentriert sich auf den Begriff des Algorithmus. Zunächst beschreibt er die Wandlung der Bedeutung des Begriffes und stellt dann kurzerhand den Euklidschen Algorithmus vor.
Der Euklidsche AlgorithmusFür alle die sich nicht erinnern:
Die natürlichen Zahlen n und m seien die, deren größten gemeinsamen Teiler wir suchen. Nehmen wir an n ist die größere Zahl.
1. r:=n-m
2. Ist r=0? Dann fertig. Ergebnis ist n (=m).
3. Ist r>=m? Dann n:=r. Sonst m:=r.
4. Zurück zu 1.
(Danke an Sebi, der hier den Fehler gefunden hat.)
Zu der Erläuterung der Programms zeichnet Knuth noch einen Programm-Ablauf-Plan (PAP). Da sich meine Version des Algorithmus leicht von seiner unterscheidet, habe ich auch ein eigenes Flussdiagramm:
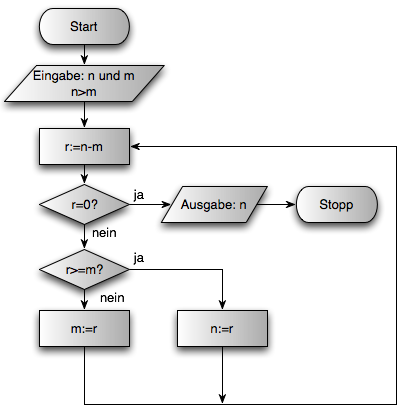Kriterien für einen AlgorithmusKnuth und Wikipedia sind sich darin einig, fünf Eigenschaften als für Algorithmen charakteristisch zu benennen: Endlichkeit der Beschreibung, Bestimmtheit der Schrittfolge, Eingabe von Daten, Ausgabe von Daten und Effektivität der Schritte. Letzteres kann man etwa so umschreiben, dass die Beschreibung ausschließlich klare, durchführbare Schritte enthält.
Da diese Definition für den mathematisch orientierten Geist vielleicht ein wenig zu prosaisch und unscharf ist, hat Knuth am Ende des einleitenden Abschnitts etwas vorgestellt, das er Berechnungsmethode nennt.
Berechnungsmehtode/BerechnungsprozessKnuths Berechnugsmethode ist ein 4-Tupel (die genaue Definition erspare ich mir hier erstmal). Dh. es ist ein Verbundobjekt aus mehreren Teilen: Symbolen für die Eingaben, Ausgaben und Zwischenschritte und einer mathematischen Funktion, die die Abbildung von einem Schritt in den nächsten definiert.
Einerseits kann man hier eine gewisse Ähnlichkeit zu Broys Begriff der Informationsverarbeitung finden, andererseits ist die Definition sehr formal und steht im starken Kontrast zu der in „Structure and Interpretation of Computer Programms“ zu findenden Definition eines Berechnungsprozesses:
Wir sind im Begriff die Idee eines Berechnungsprozesses zu studieren. Berechnungsprozesse sind abstrakte Geschöpfe, die Computer bewohnen. [...] Wir beschwören die Geister der Maschine mit unseren Zaubersprüchen.
Wie man erkennt ist das Buch, das sich viel mit funktionaler Programmierung in Scheme beschäftigt, ein humorvolles und recht lebenslustiges Werk. Es ist für ein Technik-Buch ungewöhnlich kurzweilig, ohne dabei oberflächlich zu sein. Tatsächlich werden dort sehr effektive und fortschrittliche Techniken behandelt, die sich sonst in Grundlagenliteratur nicht finden.
Mathematische GrundlagenDie einzelnen Themen des entsprechenden Abschnitts bei Knuth will ich hier nicht beschreiben. Im ersten Teil erklärt er die vollständige Induktion und wendet sie gleich zu einem Terminations- und Programmbeweis an. Das ist im Normalfall eher ein fortgeschritteneres Thema, auf das wir bei Gelegenheit bestimmt noch genauer eingehen werden.
LiteraturAbelson, Sussman 1985. Structure and Interpretation of Computer Programs, New York: MacGraw-Hill
Broy, 1992, Informatik - Eine grundlegende Einführung, Berlin Heidelberg: Springer-Verlag
Knuth, 1997, The Art Of Computer Programming, Boston: Addison-Wesley